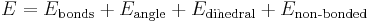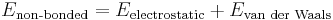Molecular modelling
Molecular modelling encompasses all theoretical methods and computational techniques used to model or mimic the behaviour of molecules. The techniques are used in the fields of computational chemistry, computational biology and materials science for studying molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling techniques is the atomistic level description of the molecular systems; the lowest level of information is individual atoms (or a small group of atoms). This is in contrast to quantum chemistry (also known as electronic structure calculations) where electrons are considered explicitly. The benefit of molecular modelling is that it reduces the complexity of the system, allowing many more particles (atoms) to be considered during simulations.
Contents |
Molecular mechanics
Molecular mechanics is one aspect of molecular modelling, as it refers to the use of classical mechanics/Newtonian mechanics to describe the physical basis behind the models. Molecular models typically describe atoms (nucleus and electrons collectively) as point charges with an associated mass. The interactions between neighbouring atoms are described by spring-like interactions (representing chemical bonds) and van der Waals forces. The Lennard-Jones potential is commonly used to describe van der Waals forces. The electrostatic interactions are computed based on Coulomb's law. Atoms are assigned coordinates in Cartesian space or in internal coordinates, and can also be assigned velocities in dynamical simulations. The atomic velocities are related to the temperature of the system, a macroscopic quantity. The collective mathematical expression is known as a potential function and is related to the system internal energy (U), a thermodynamic quantity equal to the sum of potential and kinetic energies. Methods which minimize the potential energy are known as energy minimization techniques (e.g., steepest descent and conjugate gradient), while methods that model the behaviour of the system with propagation of time are known as molecular dynamics.
This function, referred to as a potential function, computes the molecular potential energy as a sum of energy terms that describe the deviation of bond lengths, bond angles and torsion angles away from equilibrium values, plus terms for non-bonded pairs of atoms describing van der Waals and electrostatic interactions. The set of parameters consisting of equilibrium bond lengths, bond angles, partial charge values, force constants and van der Waals parameters are collectively known as a force field. Different implementations of molecular mechanics use different mathematical expressions and different parameters for the potential function. The common force fields in use today have been developed by using high level quantum calculations and/or fitting to experimental data. The technique known as energy minimization is used to find positions of zero gradient for all atoms, in other words, a local energy minimum. Lower energy states are more stable and are commonly investigated because of their role in chemical and biological processes. A molecular dynamics simulation, on the other hand, computes the behaviour of a system as a function of time. It involves solving Newton's laws of motion, principally the second law, 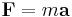 . Integration of Newton's laws of motion, using different integration algorithms, leads to atomic trajectories in space and time. The force on an atom is defined as the negative gradient of the potential energy function. The energy minimization technique is useful for obtaining a static picture for comparing between states of similar systems, while molecular dynamics provides information about the dynamic processes with the intrinsic inclusion of temperature effects.
. Integration of Newton's laws of motion, using different integration algorithms, leads to atomic trajectories in space and time. The force on an atom is defined as the negative gradient of the potential energy function. The energy minimization technique is useful for obtaining a static picture for comparing between states of similar systems, while molecular dynamics provides information about the dynamic processes with the intrinsic inclusion of temperature effects.
Variables
Molecules can be modelled either in vacuum or in the presence of a solvent such as water. Simulations of systems in vacuum are referred to as gas-phase simulations, while those that include the presence of solvent molecules are referred to as explicit solvent simulations. In another type of simulation, the effect of solvent is estimated using an empirical mathematical expression; these are known as implicit solvation simulations.
Applications
Molecular modelling methods are now routinely used to investigate the structure, dynamics, surface properties and thermodynamics of inorganic, biological and polymeric systems. The types of biological activity that have been investigated using molecular modelling include protein folding, enzyme catalysis, protein stability, conformational changes associated with biomolecular function, and molecular recognition of proteins, DNA, and membrane complexes.
See also
- Cheminformatics
- Computational chemistry
- Density functional theory programs.
- Force field in Chemistry
- Force field implementation
- List of molecular graphics systems
- List of nucleic acid simulation software
- List of software for Monte Carlo molecular modelling
- List of software for nanostructures modelling
- List of protein structure prediction software
- Molecular design software
- Molecular dynamics
- Molecular graphics
- Molecular mechanics
- Molecular model
- Molecular modelling on GPU
- Molecule editor
- Monte Carlo method
- Quantum chemistry computer programs
- Semi-empirical quantum chemistry method
- Simulated reality
- Software for molecular mechanics modelling
- Structural bioinformatics
References
- C.D. Schwieters, J.J. Kuszewski, N. Tjandra and G.M. Clore, "The Xplor-NIH NMR Molecular Structure Determination Package," J. Magn. Res., 160, 66-74 (2003).
- C.D. Schwieters, J.J. Kuszewski, and G.M. Clore, "Using Xplor-NIH for NMR molecular structure determination," Progr. NMR Spectroscopy 48, 47-62 (2006).
- M. P. Allen, D. J. Tildesley, Computer simulation of liquids, 1989, Oxford University Press, ISBN 0-19-855645-4.
- A. R. Leach, Molecular Modelling: Principles and Applications, 2001, ISBN 0-582-38210-6
- D. Frenkel, B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, 1996, ISBN 0-12-267370-0
- D. C. Rapaport, The Art of Molecular Dynamics Simulation, 2004, ISBN 0-521-82586-7
- R. J. Sadus, Molecular Simulation of Fluids: Theory, Algorithms and Object-Orientation, 2002, ISBN 0-444-51082-6
- K.I.Ramachandran, G Deepa and Krishnan Namboori. P.K. Computational Chemistry and Molecular Modeling Principles and Applications 2008 [1] ISBN 978-3-540-77302-3 Springer-Verlag GmbH
External links
- Center for Molecular Modeling at the National Institutes of Health (NIH) (U.S. Government Agency)
- Molecular Simulation, details for the Molecular Simulation journal, ISSN: 0892-7022 (print), 1029-0435 (online)
- The eCheminfo Network and Community of Practice in Informatics and Modeling